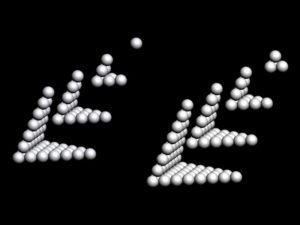Pythagorean Approach in Chemistry – Tetrahedron

Posted on December 22, 2016 by Dmitry Weise

Abstract

This work shows the possibility and applicability of the methodological approach of the ancient mathematicians to the questions raised by scientists relatively recently. The concept of figurate numbers is being applied to the problem of periodicity in the microcosm.

It is should be noted that the Pythagorean approach demonstrates the principle of simplicity, or the Principle of Parsimony in science.

Introduction

The mathematical study of figurate numbers is said to have originated with Pythagoras, possibly based on Babylonian or Egyptian precursors. Generating whichever class of figurate numbers the Pythagoreans studied using gnomons is also attributed to Pythagoras.

Gnomon

A gnomon [ˈnoʊmɒn] NO-mon, from Greek γνώμων, gnōmōn, literally “one that knows or examines”, is the part of a sundial that casts the shadow. The term has come to be used for a variety of purposes in mathematics and other fields.

Hero of Alexandria (also known as Heron of Alexandria c. 10 – c. 70 AD) defined the gnomon as that form which, when added to some form, results in a new form, similar to the original.

Non-minimal 1D gnomon – frame

The available literature says nothing about how many gnomon variations a figure can have. For a rectangle, including square, a minimal gnomon is L-shaped figure.

Fig. 1. Square composed with L-shaped gnomons: 1 + 3 + 5 + 7 = 16.

Fig. 1. Square composed with L-shaped gnomons:           1 + 3 + 5 + 7 = 16.

But the frame figure can also serve as gnomon for the rectangle.

Fig. 2. Even and odd sequences of squares. The frameworks serve as the non-minimal square gnomons.

Fig. 2. Even and odd sequences of squares. The frameworks serve as the non-minimal square gnomons.

The dimension of the gnomon is one less than the dimension of the figure itself. Gnomons for one-dimensional line (string of beads) are the points with zero dimension. Gnomon for a two-dimensional figure is a one-dimensional figure. Gnomon for volumetric figure is a plane figure.

Non-minimal 2D gnomon – shell

One can offer the concept of volume figurate number shell as the non-minimal gnomon. Shell then is a gnomon the shape of which is similar to the whole volumetric figure, but it is a hollow figure.

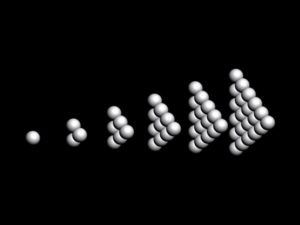
Tetrahedron

Consider a tetrahedron.

VolumeOfTheTetrahedronn = (n(n+1)(n+2))/6 = 1, 4, 10, 20, 35, 56, 84, 120, 165, … ;

n = 1, 2, 3, … .                     n – length of the edge of the figure.

If we limit the number of all possible gnomons varieties by monolayer figures, one can count 4 kinds of gnomons:

1) triangle, 2) bent square, 3) trihedral cap, 4) shell.

Gnomons-triangles

Fig. 3.  Gnomons-triangles.

The odd sequence (left) and the even sequence (right) of the bent square gnomons of the tetrahedron

Fig. 4.  The odd sequence (left) and the even sequence (right) of the bent square gnomons of the tetrahedron.

Fig. 3. Three tetrahedra sequences can be made by the trihedral cap gnomons

Fig. 5.  Three tetrahedra sequences can be made by the trihedral cap gnomons.

Fig. 4.Pyramids and their shells

Fig. 6. Pyramids and their shells.

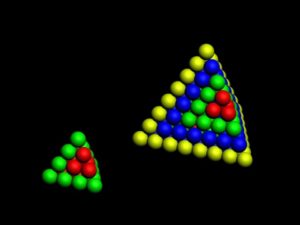
One of the four possible sequences of tetrahedron shells is:

ShellOfTheTetrahedron= 2*(2*12 + 2*22), 2*(2*32 + 2*42), 2*(2*52 + 2*62), …=

= 20, 100, 244, ….

Theorem:

In terms of figurate numbers, one can construct a sequence of tetrahedra, the shells of which are equal to the double sum of two consecutive double squares of natural numbers. What is the point of such construction?

Described structure of repeating doubled squares corresponds the structure of the table of the periodic law of elements.

Some scientists pay tribute to the table proposed by the French scholar Janet.

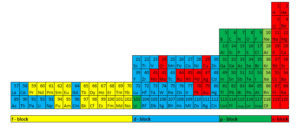Fig. 7. Periodic table of the elements based on the electronic structure of atoms. Janet (1929), Tarantola (2000), etc.

 

The length of the period in the periodic law, as is well known, is equal to 2n2.

Periods of equal length are encountered twice in the table.

Our proposition

Three-dimensional table of the periodic law can be constructed in the form of a tetrahedron having an inner order. A comparison of the tetrahedron shells and the table of elements shows, that one tetrahedron shell corresponds to 4 periods of the 2D table.

Fig. 6.Tetrahedron shells. Size: 20, 100 - Three-dimensional table of the periodic law - Model of the atom

Fig. 8. Tetrahedron shells. Size: 20, 100  – Three-dimensional table of the periodic law  –  Model of the atom.

It was also shown previously that the electron shells in the atoms and square gnomons are isomorphic [1].

Note that any modification of the periodic law table is abstract duality. On the one hand, it is simply an ordered list of existing or hypothetical elements. On the other hand, the table reflects the structural characteristics of the nucleus and electron shells of the atom. So, the number of balls in the model corresponds to the number of protons in the nucleus and electrons in orbitals. With a certain degree of abstraction our figures can be considered as a model of the atom.

REFERENCES

Weise, D. (2003): The Pythagorean approach to the problems of periodicity in chemistry and nuclear physics, In: Progress in Theoretical Chemistry and Physics, Vol.12, Advanced Topics in Theoretical Chemical Physics, Edited by Jean Maruany, Roland Lefebvre, and Erkki J. Brändas ISBN: 978-90-481-6401-1 (Print) 978-94-017-0635-3 (Online).

About Dmitry Weise

My name is Dmitry Weise. I was born on the 4th of September 1956 in Moscow. In those days, my country was called the Soviet Union. I studied in the secondary school, I loved Biology. The Soviet school gave a good and solid knowledge in those days. Then I entered and graduated from Medical University and up to date (2012) I have been working as a medical doctor. I have no special technical and mathematical education. I still keep one memory of my childhood: I enter a bookstore and see a plain little book with the abstruse name "Fibonacci numbers” on the top shelf. I thought: "Is there anybody going to read this book?" Many years later I accidentally found out that the Fibonacci numbers can be explicitly observed on the very large numbers of plants. It was probably the biggest surprise in my life. This fact was not actually described in the available literature. My familiar botanists did not know about phyllotaxis (leaves arrangement). This was very contrary to my ideas about the relationship of Wildlife and Mathematics (at my University we studied the statistics). My life has been split into two periods: before and after. I wanted to find the answer to this riddle. As an adult family man, I surprised other people by counting the spirals on pinecones, pineapples, sunflowers and other flora object. After I became acquainted with other “fibonaccists”, I learned to hide my addiction. I envy myself, recalling this period of life. I felt like a pioneer, like a discoverer in the absence ofliterature, good specialists, and The Internet. There was a new obsession, previously unknown to me. First I looked at scientists as at martyrs, and now, having experienced the joy of discovery, I began to regard them as happy people. Later I learned that most of my discoveries had already been discovered last century, but it was not disappointing for me. I thank my lucky stars that phyllotaxy-passion has helped me to understand something in the surrounding beloved nature and share my knowledge with others. I thank my lucky stars that phyllotaxy-passion has helped me to join the community of interesting and noble science people – my friends, my colleagues. Thank Symmetry!
This entry was posted in Uncategorized. Bookmark the permalink.

Leave a Reply